Уроки дизайна вышивки: симметрия
Уроки дизайна вышивки: симметрия
В этом уроке мы научимся создавать уравновешенные гармоничные композиции и откроем секрет хороших отношений в коллективе.
Что вы предпочитаете больше — конфеты или сосиски? Если бы вы были рыжим котом, думаю, что сомнений бы у вас не было. Поэтому, рассматривать понятие симметрии будем на примере с сосисками.
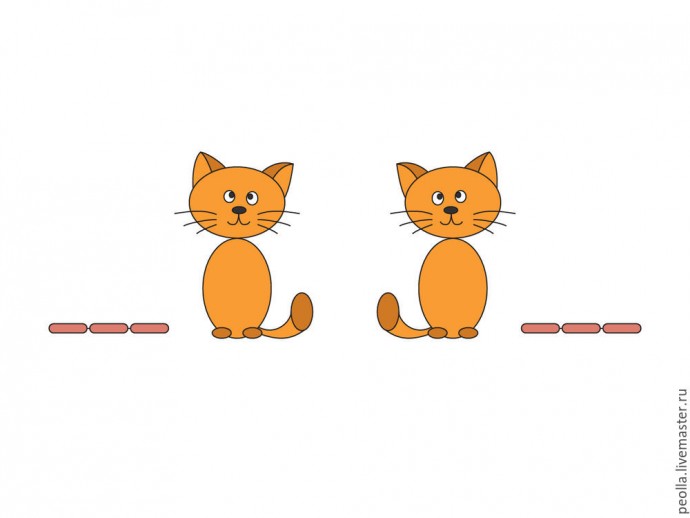
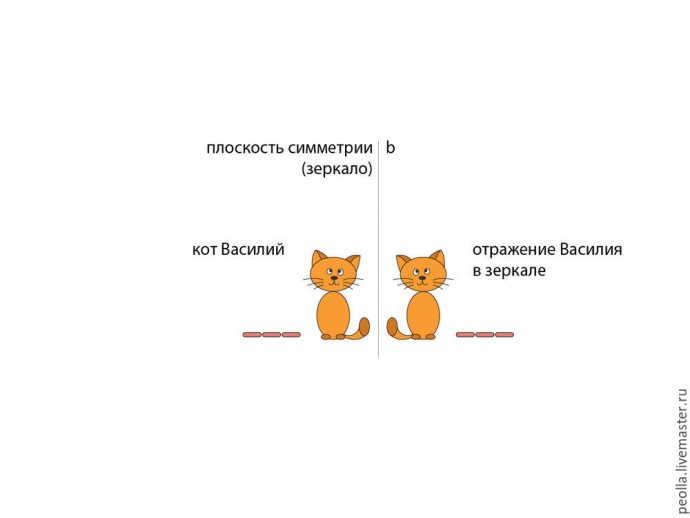
Симметрия в переводе с древнегреческого означает соразмерность, соответствие, неизменность, проявляемые при изменениях и преобразованиях чего-либо. В нашем случеае "что-либо" — это не кто-либо, а рыжий кот Василий, получивший от хозяйки за свою красоту и обаяние три свежих сосиски. Но, дело в том, что есть у него брат Кузьма, не менее обаятельный и привлекательный, но опаздавший к завтраку. На рисунке вверху вы видите их портрет. Кажется, что что-то не так, ощущается некое напряжение, назревает конфликт. В чем же причина? — в неуравновешенности, точнее в несправедливости. Усы, лапы, хвост те-же, а сосисок не дали.
Попробуем исправить ситуацию и дадим также и Кузе три свежих сосиски. — Совсем другое дело! Гармония и благодать, дружба, мир и всем хорошо. Это с кошачьей точки зрения, а с позиции геометрии, можно сказать, что мы выполнили преобразование отражения, то есть, получили зеркальную симметрию. Другими словами, если посадить Василия с сосисками рядом с зеркалом, то мы увидим в зеркале его копию, но в отраженном виде. Композиция стала абсолютно уравновешена. Древние греки часто использовали такой вид симметрии, полагая, что она олицетворяет идею гармонии и совершенства.
Если вам захочется глубоко изучить законы симметрии, то могу порекомендовать книгу: А.В. Шубников, В.А. Копцик "Симметрия в науке и искусстве". Мы же начнем с самого простого, необходимого и достаточного для создания дизайна вышивки, мы рассмотрим три вида симметрии: симметрия скольжения, отражения и вращения. Если вы со школьных времен боитесь геомерии — не бойтесь, смело пропускайте все текстовые описания и просто внимательно рассматривайте картинки — вы все обязательно поймете
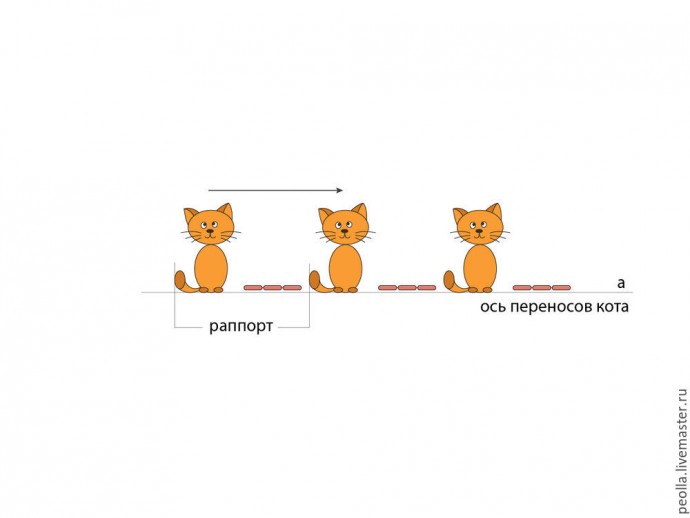
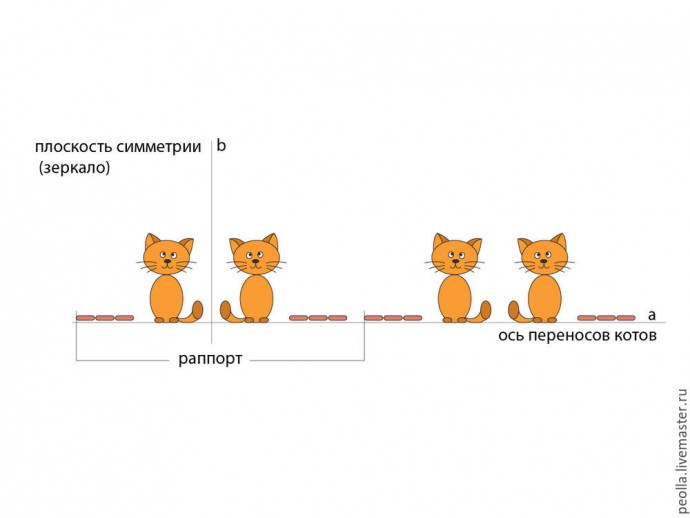
1. Симметрия скольжения. Все очень просто, объяснение смысла этого вида симметрии дано в его названии. Допустим, вы хотите сделать фото Василия, сидящего на подоконнике и, для получения прекрасного снимка, просите его пару раз немного подвинуться вдоль подоконника на некоторое одинаковое расстояние. Последовательные перемещения Василия будут выглядеть примерно так, как показано на рисунке внизу, а расстояние, на которое перемещался Василий будет называться раппортом. Сам же подоконник в данном случае будет выполнять роль прямой а, вдоль которой двигался Василий и будет называться "осью переносов", в нашем случае, осью переносов кота
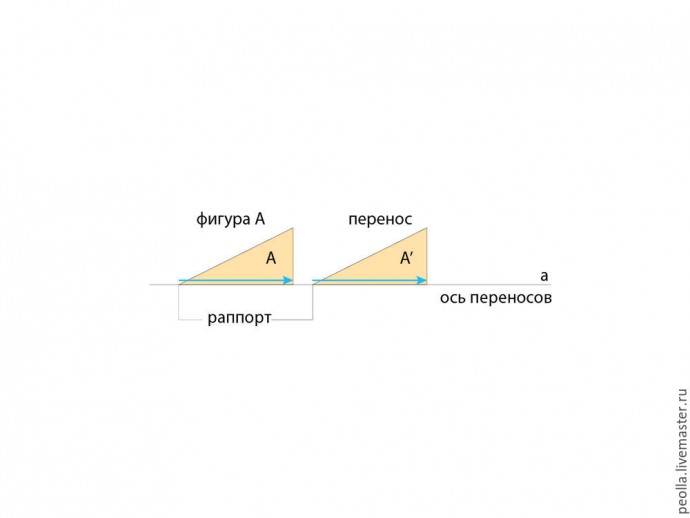
Посмотрите на рисунок внизу. Фигура А - (желтый треугольник) скользит вдоль прямой а, в результате чего мы получаем фигуру А' — точную копию фигуры А, но смещенную на расстояние раппорта. Следует уточнить, что раппорт может быть меньше, равен или больше элемента по отношению к которому выполняется преобразование скольжения. Этот вид симметрии дает ощущение движения, очень распространен и используется при построении декоративных бордюров, а также, в сочетании с другими видами симметрии, для создания более сложных композиций.
2. Симметрия отражения (зеркальная).
Этот вид симметрии мы уже рассмотрели на примере с котом Василием в начале статьи. Уточним лишь рисунок, обозначив зеркало (а еще правильнее, след плоскости зеркала на плоскости рисунка) - прямую b. В рассматриваемом примере зеркало стоит строго вертикально и перпендикулярно плоскости рисунка, поэтому мы видим лишь его торец. Отражение Василия является его точной копией, но, все что у Василия было слева — стало справа и наоборот (сосиски были слева, хвост справа, у отражения Василия все в другую сторону). Это свойство зеркала и, соответственно, зеркальной симметрии.
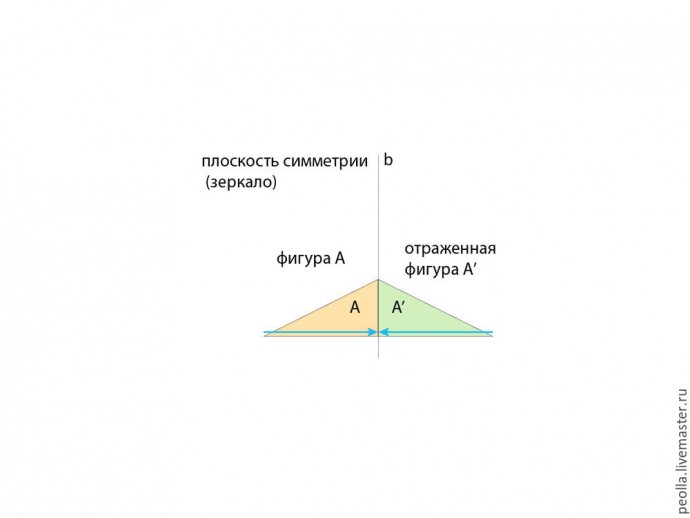
На рисунке внизу желтый треугольник (фигура А) отражается в зеркале, в результате, получаем фигуру А' - точную копию фигуры А, но, все что было слева, стало на таком же расстоянии от плоскости симметрии (прямая b) справа. Это самый распространенный вид симметрии — мы видим его повсюду в природе, а также в искусстве, технике и даже в музыке, лингвистике и других науках.
Часто симметрии отражения и скольжения используются вместе. Если вам удастся рассадить братьев Василия зеркальными парочками, затем переместить эти парочки на одинковое расстояние друг от друга, то вы получите картину небывалой красоты и умиротворения.
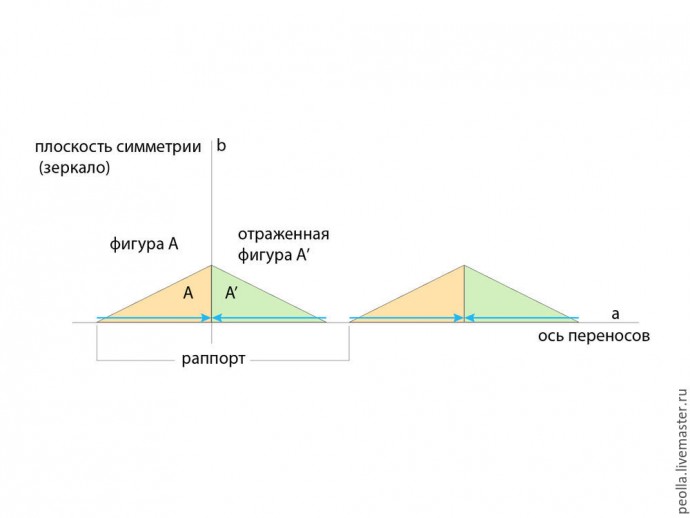
На следующем рисунке вы видите схему построений комбинированной симметрии отражения и скольжения. Вначале фигура А отражается зеркально относительно вертикальной плоскости симметрии, а затем обе фигуры (первоначальная А и отраженная А') становятся единым элементом и для этого элемента выполняется преобразование скольжения (перенос) вдоль оси а на расстояние раппорта.
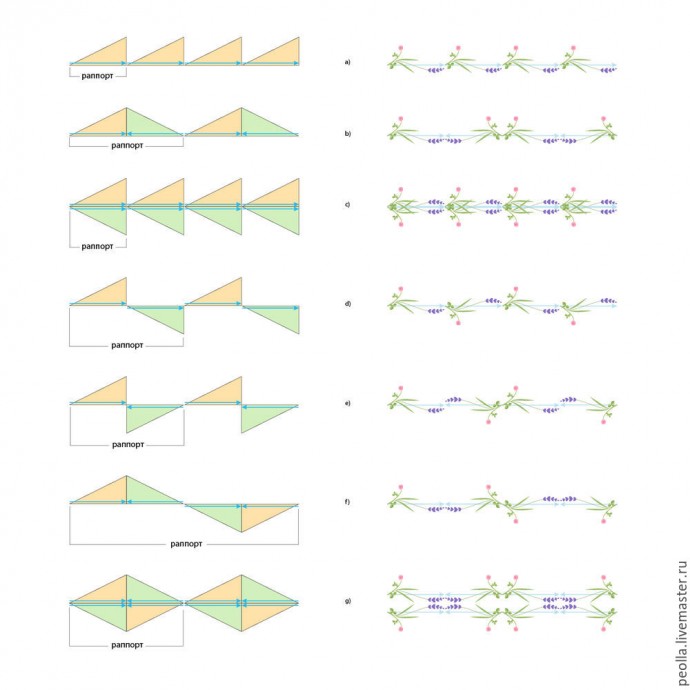
Рассмотрим варианты применения симметрий отражения и скольжения для создания декоративных бордюров. Как мы договорились ранее, желтый треугольник — первоначальная фигура, зеленый треугольник — ее зеркальное отражение (в этом примере для отражения мы будем использовать только вертикальные и горизонтальные плоскости симметрии, перпендикулярные плоскости рисунка). Заметим также, что преобразование отражения может быть выполнено с одной и той же фигурой несколько раз, то есть, например, мы можем отразить фигуру относительно вертикальной плоскости симметрии, а потом, уже отраженную фигуру еще раз отразить относительно горизонтальной плоскости симметрии. На рисунке ниже даны 7 вариантов симметрии бордюров (подробнее в книге А.В. Шубников, В.А. Копцик "Симметрия в науке и искусстве").
Справа, напротив каждого примера с треугольниками, помещен пример с растительными мотивами. Синяя стрелка на треугольниках дана для удобства восприятия, она же служит ориентиром того, как следует располагать растительные мотивы для создания бордюра с заданной симметрией.
Как видите, мы получили достаточно разнообразный набор бордюров. Обратите внимание, во всех примерах, за исключением примера а), после преобразований отражения, мы имеем уже составные мотивы, которые далее участвуют в преобразованиях переноса. Открою вам еще один большой секрет — вариантов бордюров на основе представленных схем симметрии может быть гораздо больше, если перед выполнением отражения попробовать подвигать мотив, подводя его ближе или дальше к плоскости отражения, а также прислоняя его под разными углами (в примере на рисунке использовано лишь горизонтальное положение мотивов). Кроме того, данные бордюры можно использовать для заполнения больших поверхностей, располагая их параллельными рядами.
3. Симметрия вращения.
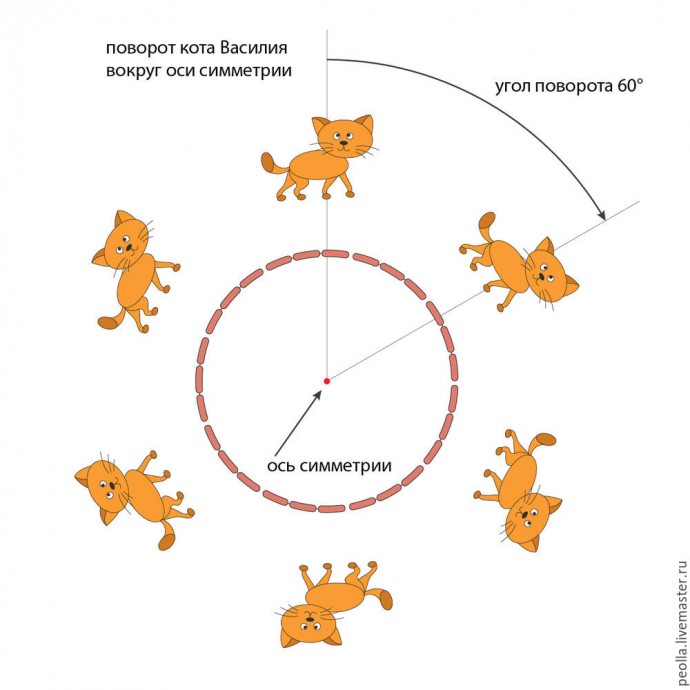
Помните, у Пушкина: "И днем и ночью кот ученый все ходит по цепи кругом...". Если нашего Василия отправить в такое путешествие вместе с его братьями, то получим вот такую картину (при условии, что они не будут догонять друг друга, а будут ходить гуськом, с одинаковым интервалом). Это и будет симметрия вращения. Точка, вокруг которой ходит Василий с братьями - на самом деле не точка, а проекция оси, перпендикулярной плоскости рисунка. Эта самая ось будет называться осью симметрии.
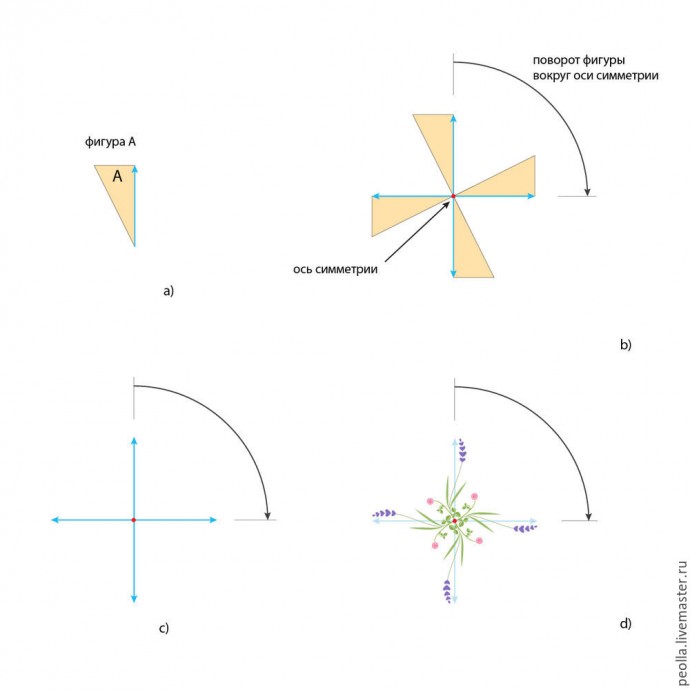
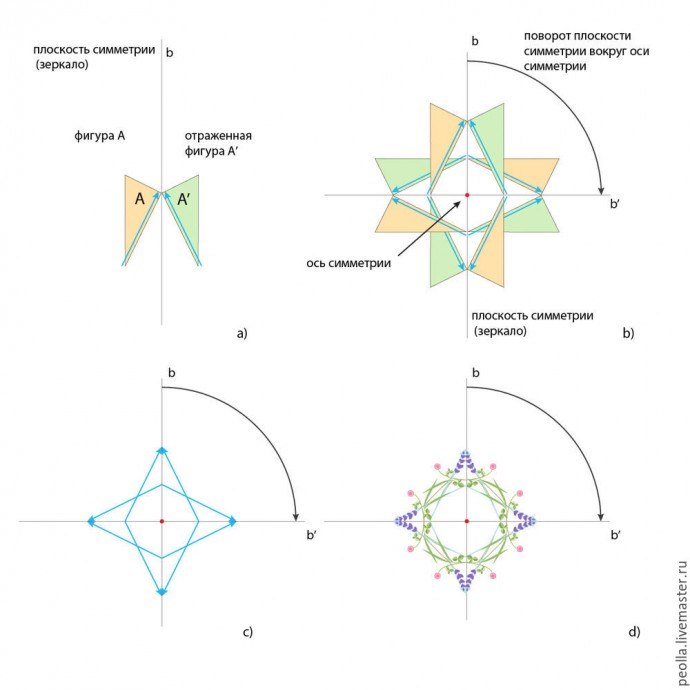
На следующем рисунке симметрия вращения рассмотрена на примере с треугольниками. Фигура А осуществляет поворот вокруг оси симметрии (красная точка). Угол поворота на этом примере равен 90°, соответственно за полный оборот вокруг оси симметрии фигура совместится сама с собой: 360° : 90° = 4 раза. На рис. с) вы видите общую схему данного преобразования. Заменив треугольники на цветочные мотивы, получим декоративную розетку (рис. d). Данный вид симметрии позволяет передать вращательное "движение" в композиции.
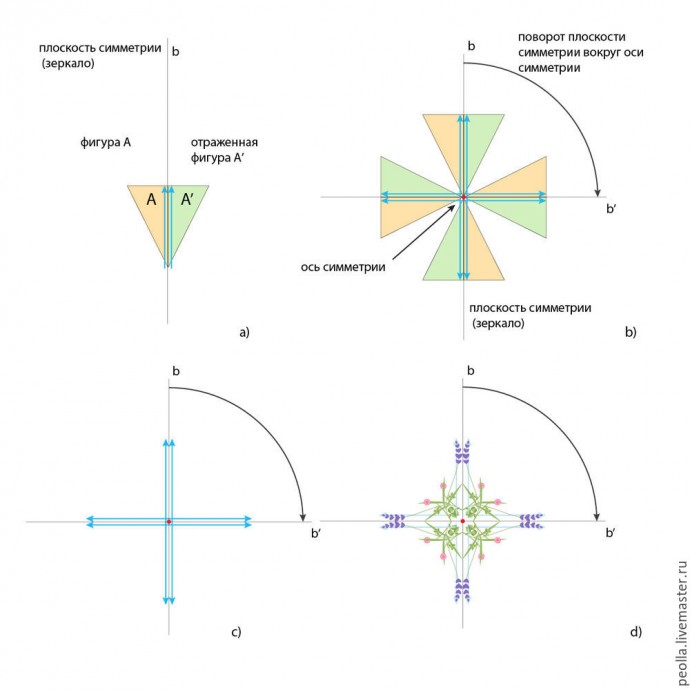
На рисунке ниже дан еще один пример симметрии вращения, но уже совмещенной с зеркальной симметрией. Первое преобразование — отражение фигуры А относительно вертикальной плоскости симметрии. Второе преобразование — вращение плоскости симметрии, фигуры А и ее отражения — фигуры А' вокруг оси симметрии. Фигуры А и А' теперь становятся единым мотивом. Как и в предыдущем примере, угол поворота равен 90°. Вообще, угол поворота может быть и другим, вы просто должны предварительно решить — сколько копий вашего мотива должно уместиться в одном полном обороте, затем разделить 360° на выбранное вами количество повторений мотива. Например, вы хотите разместить 3 мотива, расчет будет таким: 360° : 3 = 120°. Если же вы решили расположить ваш мотив 7 раз, то угол поворота должен быть: 360° : 7 = 51,43° . Скажем, не очень удобный результат, но, если у вас есть транспортир, то вы с этим справитесь. Для удобства, приведу здесь таблицу "целочисленного" деления окружности, т.е. определения угла поворота, выраженного в целых градусах.
Ниже представлен еще один вариант использования симметрии вращения и симметрии отражения. Здесь мы расположили фигуру А под углом к плоскости симметрии, получив при этом немного иной вид конечного мотива (фигура А + фигура A'). На рис. с) дана общая схема симметрии. Заменив треугольники на цветочные мотивы, получаем декоративную розетку (рис. d). Отметим, что в этом примере был использован тот же цветочный мотив, что и в предыдущем, а результаты получились разными. Как и в случае с симметрией бордюров, мы можем легко изменять положение исходного мотива относительно плоскости симметрии — двигать его ближе или дальше, поворачивать разными сторонами к плосксти симметрии. В итоге этот метод дает бесчисленное множество вариантов симметричных розеток.
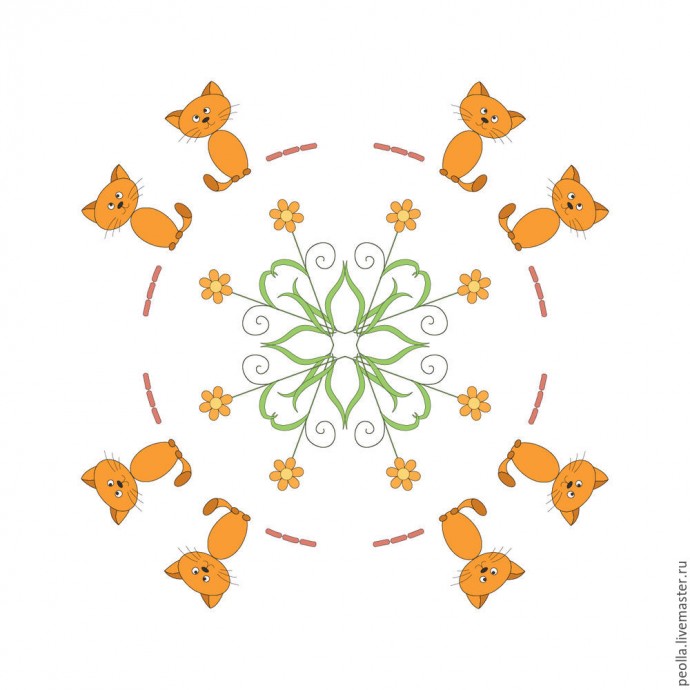
И наконец, изучив достаточно тщательно науку о симметрии котов, мы можем нарисовать великолепную картину под названием "Кошачье счастье". Таким же образом рисуются картины: "Цыплячья дружба", "Заячья радость" и др. Как видим, преобразования симметрии делают нас практически волшебниками и дают нам возможность из одного или нескольких мотивов создавать бесконечно разнообразные композиции, уравновешенные и гармоничные. Основываясь на изученных принципах вы можете придумывать также и намного более сложные конструкции, комбинируя виды симметрии и меняя мотивы.